【一】单项资产的风险和报酬
一、风险衡量方法和衡量指标
风险衡量的两类方法:
图示法–概率分布图
衡量指标–方差、标准差、变化系数
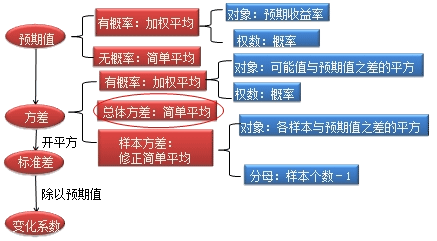
提示:
1、期望值和方差是计算基础。分两种情况:
(1)根据概率计算;在已知概率的情况下,期望值和方差均按照加权平均方法计算。
P R 偏差的平方
好 0.5 20% (20%-12%)2
中 0.3 10% (10%-12%)2
差 0.2 -5% (-5%-12%)2
预期值=0.5*20%+0.3*10%+0.2*-5%=12%
方差=偏差的平方*概率=(20%-12%)2*0.5+(10%-12%)2*0.3+(-5%-10%)2*0.2=0.00782
标准差=0.00782开平方=8.84%
变化系数=标准差/预期值=8.84%/12%=0.7
(2)根据历史数据计算。在有历史数据的情况下,期望值为简单平均;标准差为修正简单平均
20% (20%-16%)2
18% (18%-16%)2
16% (16%-16%)2
14% (14%-16%)2
12% (12%-16%)2
预期值=(20%+18%+16%+14%+12%)/5=16%
方差={(20%-16%)2+…..+(12%-16%)2}/(5-1)=0.004
标准差=0.004开平方=6.32%
变化系数=6.32%/16%=0.395
二、指标特征
指标 特征
预期值(期望值、均值):反应预计收益的平均化,不能直接用来衡量风险
方差σ2:当预期值相同时,方差越大,风险越大
标准擦σ:当预期值相同时,标准差越大,风险越大
变化系数:变化系数衡量风险不受预期值是否相同的影响
【二】投资组合的风险和报酬
投资组合理论认为,若干种证券组成的投资组合,其收益是这些证券收益的加权平均数,但是其风险不是这些证券风险的加权平均风险,投资组合能降低风险。
一、证券组合的预期报酬率
投资组合的预期报酬率等于组合中各单项资产报酬率的加权平均值。
R–报酬率 M–投资
投资M1,获得报酬M1*R1,投资M2,获得报酬M2*R2
组合报酬率=((M1*R1)+(M2*R2))/(M1+M2)
分析:证券组合的预期报酬率介于最高报酬率与最低报酬率之间,当全部资金投资于最高报酬率的资产时,该组合为最高报酬率组合;当全部资金投资于最低报酬率资产时,该组合为最低报酬率组合。
二、两项资产的风险计量
组合风险的大小与两项资产收益率之间的变动关系(相关性)有关。反应资产收益率之间相关性的指标是协方差和相关系数。
1、协方差σ12=Σ((报酬率-偏差)*(报酬率-偏差))/(n-1)
协方差为正,表示两项资产的报酬率呈同方向变化;
协方差为负,表示两项资产的报酬率呈反方向变化;
协方差为绝对数,不便于比较,再者算出某项资产的协方差为某个值,但这个值是什么含义,难以解释。为客服这些弊端,提出了相关系数这一指标。
2、相关系数
σ12=R12*σ1*σ2
r12=σ12/σ1σ2
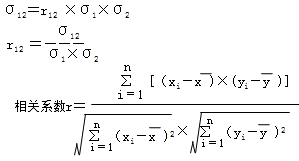
(1)相关系数大小在-1和1之间
(2)相关系数=-1,表示一种证券报酬的增长与另一种证券报酬的减少成比例
(3)相关系数=1,表示一种证券报酬率的增长与另一种证券报酬率的增长呈比例
3、两项资产组合的方差和组合的标准差
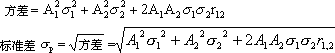
方差=a1平方σ1平方+a2平方σ2平方+2a1σ1a2σ2r12(a1和a2是投资比例)
标准差σp=方差开平方
(1)当r=+1时,标准差σp=(σ1+σ2)/2
(2)当r=-1时,标准差σp=绝对值(σ1-σ2)/2
当r=1或-1时,说明是等比例投资
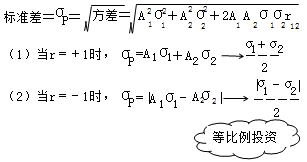
【三】多项资产组合的风险计量
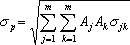
结论:充分投资组合的风险,只受证券之间协方差的影响,而与各证券本身的方差无关。
【四】两种证券组合的机会集与有效集
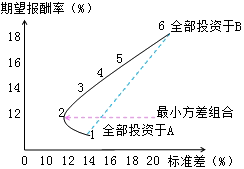
该图的几个主要特征
1、揭示了分散化效应
2、表达了最小方差的组合
3、表达了投资的有效集合
【相关性对机会集和有效集的影响】

相关系数=1,不具有风险分散化效应。
相关系数<1,机会集为一条曲线,当相关系数足够小,机会集曲线向左侧凸出。
相关系数越小,风险分散效应越强;相关系数越大,风险分散效应越弱
由两项资产构成的投资组合,其最高、最低预期报酬率组合点,以及最大方差组合点不变,但最小方差的组合点却可能是变化的。
机会集不向左侧凸出–有效集与机会集重合。最小方差组合点为全部投资于A,最高预期报酬率组合点为全部投资于B。不会出现无效集。
机会集向左侧凸出–出现无效集。最小方差组合点不是全部投资于A,最高预期报酬率组合点不变。
【五】多种证券组合的机会集与有效集
两种证券组合,机会集是一条曲线。如果多种证券组合,则机会集为一个平面。
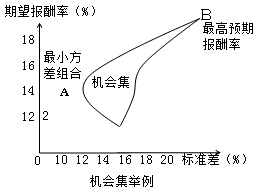
1、多种证券组合的机会集是一个平面。
2、最小方差组合是图中最左端的点,它具有最小组合标准差。
3、最小方差组合点至最高预期报酬率点的部分,为有效集(有效边界)。图中AB部分即为有效边界,它位于机会集的顶部,投资者应在有效集上寻找投资组合。
【六】资本市场线
前面研究的是风险资产的组合,现实中还存在无风险资产。在投资组合研究中,引入无风险资产,在风险资产组合的基础上进行二次组合,这就是资本市场线所要研究和解决的问题。
假设存在无风险资产。投资者可以在资本市场上借到钱,将其纳入自己的投资总额;或者可以将多余的钱贷出。无论借入和贷出,利息都是
转载请注明:八度生活 » 注会财务管理第四章第二节风险与报酬